Actividad parábolas

PREGUNTAS

1. ¿ Cómo se gráfica la función cónica " Parábola" ?

Se denomina sección cónica (o parábola cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del eje del cono (β), pueden obtenerse diferentes secciones cónicas, a saber:

• β < α : Hipérbola (naranja)

• β = α : Parábola (azulado)

• β > α : Elipse (verde)

• β = 90º: Circunferencia (un caso particular de elipse) (rojo)

• Y β= 180º : Triangular

• Cuando β > α la intersección es un único punto (el vértice).

• Cuando β = α la intersección es una recta generatriz del cono (el plano será tangente al cono).

• Cuando β < α la intersección vendrá dada por dos rectas que se cortan en el vértice.

• Cuando β = 90º El ángulo formado por las rectas irá aumentando a medida β disminuye,cuando el plano contenga al eje del cono (β = 0).

EJEMPLO

Hallar la ecuación de la parábola de directriz $x=4$ y foco $F\left(–2,0\right)$.

1.Realizar una figura de análisis que represente los datos del enunciado:

.

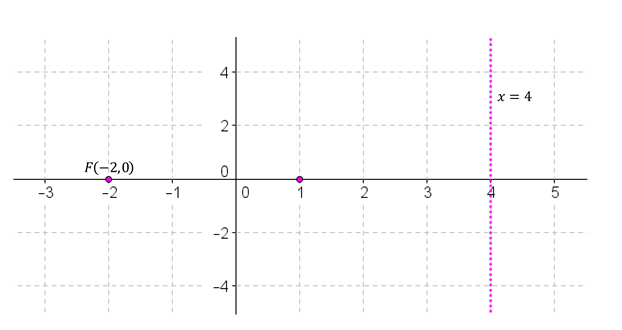
El valor absoluto de c es la distancia del vértice al foco.

$$\left|c\right|=d\left(V,F\right)$$

El vértice está sobre el eje focal y a la misma distancia del foco que de la directriz:

$$V=(\frac{–2+4}{2}$$

$$,0)=\left(1,0\right)$$

Eje focal: eje x

$x$

Como el eje es horizontal la ecuación tiene la forma:

$${\left(y–\beta \right)}^2=4c\left(x–\alpha \right)$$

$${\left(y–0\right)}^2=4c\left(x–1\right)$$

Falta calcular el valor absoluto de c

$c$

.

$$\left|c\right|=d\left(F,V\right)=3$$

Como el foco está a la izquierda del vértice entonces 

$c=–3$

.

Entonces queda:

$$y^2=–12\left(x–1\right)$$

$x$

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones.

La parábola "básica", y = x 2 , se ve así:

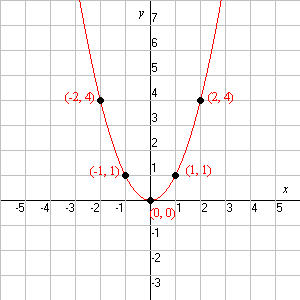
La función del coeficiente a en la ecuación general es de hacer la parábola "más amplia" o "más delgada", o de darle la vuelta (si es negativa):

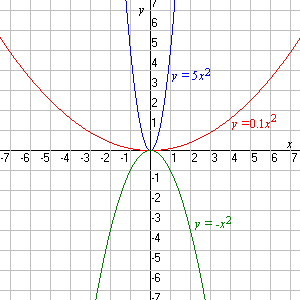
Si el coeficiente de x 2 es positivo, la parábola abre hacia arriba; de otra forma abre hacia abajo.

El vértice

El vértice de una parábola es el punto en la parte baja de la forma "U" (o la superior, si la parábola abre hacia abajo).

La ecuación para una parábola también puede escribirse en la "forma vértice":

y = a ( x – h ) 2 + k

En esta ecuación, el vértice de la parábola es el punto ( h , k ).

Puede ver como esto se relaciona a la ecuación estándar al multiplicarla:

y = a ( x – h )( x – h ) + k

y = ax 2 – 2 ahx + ah 2 + k

El coeficiente de x aquí es – 2 ah . Esto significa que en la forma estándar, y = ax 2 + bx + c , la expresión

nos da la coordenada en x del vértice .

3. ¿ Cuáles son las partes de una función cónica parábola ?

La parábola se puede considerar como una elipse, uno de cuyos vértices se encuentra en el infinito, así como el centro de la curva. Partiendo de esta consideración, comprobaremos que las propiedades enunciadas para la elipse, se cumplen igualmente en la parábola.

La circunferencia principal Cp, pasará por el vértice V de la curva, y dado que el centro de la curva se encuentra en el infinito, la circunferencia principal resulta ser la recta perpendicular al eje en el vértice V. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la parábola. También se puede definir como el punto medio de los segmentos que unen el foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la parábola.

La única circunferencia focal Cf de la parábola, tendrá su centro en el infinito, y deberá pasar por el punto D, simétrico del foco respecto a la tangente el en vértice de la curva, resultando por tanto, una recta coincidente con la directriz de la parábola. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del foco F, respecto a las tangentes (t) de la parábola.

Observando la figura, también podemos definir la parábola, como el lugar geométrico de los centros de circunferencia que pasan por el foco F, y son tangentes a la circunferencia focal.